问题
最近做的项目中经常会在C++环境下和高精度的double浮点类型数据打交道
这些double类型数据精度级别可能到 pico级别(10^-12) 甚至 femto级别(10^-15),用来表示集成电路的一些微观属性
但是非常诡异的是,不知道为什么在对这些高精度的浮点数进行运算时,往往最后运算产生的数据会和你预期的不一样。比如下面这些场景
1:使用double数据进行大小判定踩的坑
我有两个double 类型数据val1 和val2,经过运算后 能够确定的是它们大小是相等的 按照预期 val1 = val2= 1.0000000025 但是用if( val1 == val2 )去做相等判定的时候 得到的结果却是false2:使用QDoubleSpinBox获取数据时踩的坑
QDoubleSpinBox是QT库中的一个可调节数值大小的文本框 QDoubleSpinBox有一个value接口可以用来获取当前显示的值 假设此时文本框显示的值时0.0000000267 当我用value()获取这个值,赋值给val1 并且用if( val1 == 0.0000000267)判定时返回false3:使用QDoubleSpinBox设定数据进行运算时踩的坑
QDoubleSpinBox可以通过setValue()接口设定要显示的值 当我用setValue(0.000000102)时 最后显示的结果时0.00000010200014:使用std::to_string数据进行运算时踩的坑
最后res的结果不是0.23165498 ,而是0.231654981
2double val = 0.23165498;
auto res = std::to_string(0.23165498);5:使用double数据进行运算时踩的坑
1
2double val = 0.00000104;
val = val / 10;最后val的结果是0.0000001040001
踩了很多的坑,后来了解了一下原因
发现
原来计算机在记录这些浮点类数据的时候 ,用的记录方式本身就是不精确的,也就是说double类型数据本质上自带误差的比如你定义了
float fval = 0.45,但其实它的真实值为0.449999988。定义了double dval = 0.45 但它的真实值为0.45000000000000001这是为什么呢?
原因
要想详细的解释上面的现象出现的原因,就得聊聊计算机是怎么存储浮点数的
以下内容引用自https://cloud.tencent.com/developer/article/1473541
发现这位horstxu大佬写的很好。在编程中,浮点类型数据主要用于表示小数,例如Java或C++中的float、double类型,Golang中的float32、float64类型。我们在开始学编程的时候也经常被教育,浮点数有精度问题,不适用于比较大小或比较相等性的逻辑。任何数字在计算机中都是用0和1二进制来表示,对于float(占据4字节)和double(占据8字节)类型,又是如何使用一串0和1表示出来呢?
浮点数的存储方案是来自于IEEE 754(IEEE Standard for Floating-Point Arithmetic)标准,这一标准最早在1985年提出,基本上已经被用于所有计算机中。IEEE 754经历了几次标准更新,但是最核心的内容,即浮点数表示规则,从来没有变过。该标准一共经历了1985版,1987版,2008版,2019版等几个版本的更新,最新版2019版的官网链接在此:https://standards.ieee.org/content/ieee-standards/en/standard/754-2019.html ,感兴趣的话可以延伸阅读。
要表示浮点数的第一步,就是让小数也能使用二进制来表示。我们知道二进制表示整数时,最低位代表2的0次方,往高位依次是2的1次方,2次方,3次方……那么对应的,二进制数小数点后面,最高位则是2的-1次方,-2次方,-3次方……如下图所示:

- 二进制浮点数每一位对应的十进制数值
下面举几个例子:

十进制与二进制转换
十进制数字10.625,用二进制表示为1010.101 。其实这种二进制表示小数的方法,造成了一个隐含的问题:一些本来不是无限循环的十进制小数,表示成二进制之后成了无限循环小数。比如上图中的十进制数字0.6,表示成二进制之后成了循环体为1001的无限循环小数。这就是“浮点数有精度问题”的根源之一,你在代码中声明一个变量double a = 0.6;时,计算机底层其实是无法精确存储那个无限循环二进制数的,只能存一个四舍五入(准确说应该是零舍一入,毕竟是二进制)后的近似值。下一步,将二进制表示为以2为底的科学计数法,如图:

- 二进制科学计数法
对于任何数字表示成二进制科学计数法以后,一定是1点几(尾数)乘以2的多少次方(指数)。对于小于零的负数来说,就是负1点几(尾数)乘以2的多少次方(指数)。所以要存这个数,需要存储三个部分:正负号,尾数,指数。

- 浮点数在内存中的表示方式
具体存储方式如上图所示。最高位有1bit存储正负号,然后指数部分占据8bits(4字节)或11bits(8字节),其余部分全都用来存储尾数部分。对于指数部分,这里存储的结果是实际的指数加上偏移量之后的结果。这里设置偏移量,是为了让指数部分不出现负数,全都为大于等于0的正整数。尾数部分的存储,因为二进制的科学计数法,小数点前一定是1开头,因此我们尾数只需要存储小数点后面的部分即可。接下来依然是举例说明:

4字节浮点数0.6的存储方式
再来看一个8字节浮点数的例子:

8字节-0.1的存储方式
8字节数字-0.1,可以看到最高位为1,表示负数。后面逻辑和前文的4字节浮点数类似,只是偏移量略有区别。浮点数的这种表示法,其实对于绝对值比较大的数来说,小数点后面的精度会比较差。对于绝对值接近0的比较小的数来说,小数点后面的精度反而会非常高。我们用一段简单的golang代码来说明一下(非常简单,非golang开发也能看懂)。
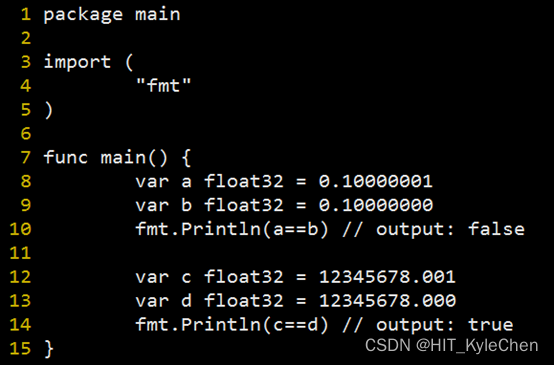
浮点数的相等性比较
我们可以看到,变量a和b的差距只有0.00000001,但是他们在内存中所存储的值依然是不同的,a和b比较会返回false。但是对于c和d来说,他们值只差了0.001,小数点后的差距比a和b的差距要大很多,c和d的判断结果依然是相等。这是由于c和d整数部分占据了4字节太多位置,导致小数部分的数值差距,在4字节内已经体现不出来了。c和d在内存中存的值是完全一样的。前文所说的零舍一入机制,加上浮点数在内存中本身的存储机制,导致了我们编程中经常被提醒的:“浮点数有精度问题”。由此我们也就知道了为什么double类型数据会在加减乘除计算和字符串转换过程中产生精度误差 。主要是由于浮点数在计算机内部的二进制表示与实际小数值之间存在的差异,这种差异通常被称为“舍入误差”。舍入误差会在多次运算中积累,从而导致误差不断放大。例如,两个看似相等的浮点数进行运算时,其结果可能会因为舍入误差而不同。
措施
1. 如何对浮点类型数据做相等判定?
在最开始说到的问题1 和问题2都是和double数据相等判定相关的问题
对于浮点类型数据做相等判定
我们可以提前定义一个确定大小的误差值,当val1 和 val2的差绝对值小于这个误差值的时候就认定位相等
1 | #define eps 1e-6 |
boost库中好像有一些API把两个值之间的差计算到精度级别
2. 如何让QDoubleSpinBox精确的显示浮点类型数据?
- 这里说的精确其实只是一种规避手段,并不能真正做到精确
我们可以使用QDoubleSpinBox的setDemical接口去设定显示在文本框中数据的小数点后面的位数
比如setDemical(5)则表示我们只会用四舍五入的方式显示原数据小数点后面的5位
只要前5位小数是精确的,那么显示在文本框上的数据就是精确的
3. 如何有效的将浮点数转为字符串?
sprintf函数
这里不细说std::to_string
std:to_string()方法只能精确到6位小数点
1
2
3double d = 3.1415926535897932384;
std::string str = std::to_string(d);
std::cout << str << std::endl; // 3.141593std::stringstream
使用stringstream,在输入流时使用setprecision设置精度
注意头文件要包含下面两个1
2
3
4
5
6#include <sstream>
#include <iomanip>
std::stringstream ss;
ss << std::setprecision(15) << d;
str = ss.str(); // 3.14159265358979std::setprecision如果设定大于15那么后面的数据会不可靠
关于std::stringstream和 std::to_string更详细的讲解可以看这篇文章 https://www.cnblogs.com/chorulex/p/7660187.html
4. 如何有效的解决浮点数在运算时产生的精度误差
不能完全解决 只能尽量缓解
尽量避免直接进行连续的加减乘除操作,而是采用累加器或积累器等数据结构,减少中间结果的累计误差。
利用算术运算法则,将算式转换为更加稳定的计算方式。例如,可以将 A/B * C 转换为 A * (C/B),或者将 A/C * B 转换为 A * (B/C)。
使用高精度库(如 GMP、MPFR 等)或自定义实现高精度运算的数据结构,来代替原本的浮点数类型进行计算。
在具体问题中选择合适的计算精度。例如,在实现一个简单的计算器时,可以将小数部分保留 4-5 位来避免累计误差。
了解浮点数的特性和运算规则,合理利用舍入误差和向零取整等特性,减小误差的产生。例如,在求平均数时采用 Kahan 总和算法等技巧,可以有效减少舍入误差对结果的影响。
需要根据具体的问题和实际情况来选择合适的方法,以达到减小误差、提高计算精度的目的。